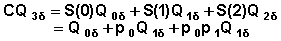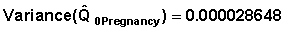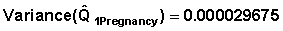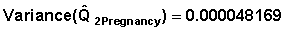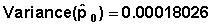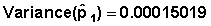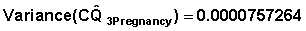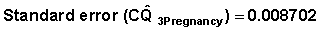Lesson 7: Multiple-Decrement Life Tables with Observational Data
7.0 Overview
In Lesson 6, we learned to construct single decrement life tables with observational (micro) data. In this session we will learn how to extend the method to construct multiple decrement life tables.
Recall that in a multiple decrement life table individuals leave a well-defined cohort through multiple attrition factors. For example, a group of married women can end their marriage by divorce or widowhood. A single decrement life table does not distinguish between divorce and widowhood, but combines them to form a single attrition factor, "marital disruption." In an ordinary life table, we considered discontinuation of pill use without taking into account the reason for discontinuation. In a multiple decrement life table, we will differentiate various reasons for the discontinuation of pill use.
Download a zip file containing data for Lesson 4 in Excel and CSV formats.
7.1 Examples of Data
Data 1: Study of Marital Disruption
Table 7.1 shows tabulations of marital disruption by cause from a demographic survey of 17,045 ever-married women. This data set is the same as the data set 1 we used in constructing the single decrement life tables except that the marital disruption is now separated into divorced or widowed.
| Table 7.1: Marital Disruption by Cause and Duration of Marriage | |||||
Duration of Marriage in Completed Years | Number Divorced | Number Widowed | Number of Marital Disruptions | Number Still Married at Survey | Total |
|---|---|---|---|---|---|
| 0 | 140 | 1 | 141 | 88 | 229 |
| 1 | 211 | 3 | 214 | 222 | 436 |
| 2 | 272 | 2 | 274 | 523 | 797 |
| 3 | 256 | 8 | 264 | 405 | 669 |
| 4 | 232 | 12 | 244 | 452 | 696 |
| 5 | 193 | 10 | 203 | 555 | 758 |
| 6 | 193 | 13 | 206 | 539 | 745 |
| 7 | 174 | 12 | 186 | 543 | 729 |
| 8 | 147 | 19 | 166 | 465 | 631 |
| 9 | 142 | 18 | 160 | 435 | 595 |
| 10 | 122 | 18 | 140 | 441 | 581 |
| 11 | 96 | 20 | 116 | 437 | 553 |
| 12+ | 981 | 113 | 1094 | 8532 | 9626 |
Total |
3159 |
249 |
3408 |
13637 |
17045 |
Table 7.1 shows that among 17,045 ever-married women interviewed, 141 ended their first marriage in the first year, 140 of them due to divorce and one due to widowhood. As before, 88 women who were married less than one year at the time of survey and still in intact marriages are considered "censored."
Essentials of a Multiple Decrement Life Table
Recall that a multiple decrement life table includes a number of summary measures. Following is a brief review of each of quantities, including the computational formulae and examples.
- Crude probability is the probability of an event due to a specific cause in the presence of other competing events.
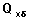 denotes the crude probability of the occurrence of an event of type
denotes the crude probability of the occurrence of an event of type 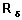 at duration x in the presence of other competing causes.
at duration x in the presence of other competing causes.
In the data above, there are two competing causes of marital disruption: divorce and widowhood. Qxd denotes the crude probability that a marriage will end at duration at x due to divorce for those in intact marriages at this duration when both divorce and widowhood are possible. Similarly one can define crude probability of widowhood and denote it as Qxw.
-
Total probability is the probability of occurrence of an event regardless of the type of event. In the above example, total probability, or qx, is the probability of a marital disruption due either to divorce or widowhood. It follows that:
qx = Qxd + Qxw
When more than two types of events occur, one can extend the above formula to calculate total probability as:
qx = Qx1 + Qx2 + ... + Qxk, where k denotes the number of possible types of events.
Remark
A slight change in the notation will be used when referring to interval data. In this case the probability of occurrence of an event of type Rs in an interval [x, x + n] will be denoted as 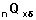 . Then the probability of an event of any type in the interval is the total probability, denoted as (nqx) and calculated in relation: (nqx) = Qx1 + Qx2 + ... +Qxk
. Then the probability of an event of any type in the interval is the total probability, denoted as (nqx) and calculated in relation: (nqx) = Qx1 + Qx2 + ... +Qxk
Survival Function
A survival function is the probability of no event of any type by duration x. As before, this function is denoted asS(x) and calculated using the Kaplan Meier estimate as:
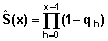
In order to interpret the multiple decrement life easily use another quantity lx = 100,000 x S(x) . Because S(0) = 1,l0 = 100,000 and one can interpret l0 as the radix of the life table.
Occurrence of Events of Particular Type at a Specified Duration x
In the life table population with the radix of 100,000, there will be some events of a particular type at each duration. We denote 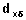 as the number of occurrences of event type
as the number of occurrences of event type 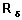 at duration x. The number of events of a specific type
at duration x. The number of events of a specific type 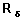 is obtained as:
is obtained as:
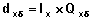
Note that the total number of events of all types at duration x will be:
dx = dx1 + dx2 + .... + dx2.
Cumulative Number of Events of a Particular Type by a Specified Duration
Denote 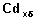 as the cumulative number of events of type
as the cumulative number of events of type 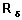 up to duration x.
up to duration x.
Then 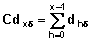
Cumulative Probability of Occurrence of an Event of Specified Type by Duration
Denote 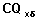 as the cumulative probability that an event of particular type will occur by duration x. By definition:
as the cumulative probability that an event of particular type will occur by duration x. By definition:
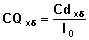
Computational Formula (Exact event times)
Step 1:
Like in the construction of the ordinary life table, first calculate the number in the risk set at specified durations. Let Nx denote the number in the risk set at duration x. Use the observed events and censoring at duration x to calculate the risk set. Like before, denote the number of events and censoring at duration x as dx and Cxrespectively. Then Nx+1 = Nx - dx - Cx
|
Example In Table 7.1 No. At duration zero, 141 individuals experienced marital disruption and 88 individuals were censored. Therefore, the number in the risk set at duration one is: N1 = 17045 - 141 - 88 = 16816 Column 2 in Table 7.2 shows the risk set at all durations.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Step 2: Computation of the crude probabilities
The notation 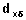 denotes the number of occurrences of events of type
denotes the number of occurrences of events of type 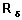 at duration x. Using this notation, the crude probability is calculated as:
at duration x. Using this notation, the crude probability is calculated as:
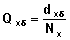
|
Example Tables 7.1 and 7.2 show N0 = 17045, 40 marital disruptions due to divorce and one due to widowhood. With this data we can calculate the crude probability of marital disruption due to divorce (Qod) and due to widowhood (Qow) as follows: Similarly crude probabilities at duration one are calculated as: The crude probabilities at all durations are shown in Table 7.2. |
Step 3: Total probability
By definition the total probability is the sum of all crude probabilities at a specified duration. Thus:
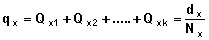
|
Example In Table 7.2 there are only two competing events for marital disruption (divorce and widowhood). Table 7.2 shows:
q1 = Q1d + Q1w = 0.012548 + .00018 + 0.01273 The total probabilities for all durations are shown in Table 7.2. |
Step 4: Computation of survival probabilities
We will use the Kaplan-Meier formula to compute the survival probabilities (probability of nonoccurence of any event by duration x).
Recall that the survival probability is calculated by the formula:
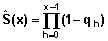
Remember that S(0) = 1.
|
Example From Table 7.2 S(0) = 1; S(1) = 1 — .00827 = 0.99173. The survival functions at all durations are given in Table 7.2. |
Step 5: Number of events of specific type
For computational ease we will create a life table lx S(x) column by multiplying the survival function S(x) by 100,000:
lx = 100000×S(x)
Then the number of occurrences of events of a specific type 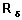 in the life table population is obtained by multiplying the lx column by the corresponding crude probability:
in the life table population is obtained by multiplying the lx column by the corresponding crude probability:
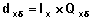
|
Table 7.3: Multiple Decrement Life Table for Marital Disruption
|
|||||||
| Duration of Marriage in Completed Years | lx | dxd | dxw | dx | F(x, d) | F(x, w) | F(x) |
|---|---|---|---|---|---|---|---|
| 0 | 100,000 | 821 | 6 | 827 | 0 | 0 | 0 |
| 1 | 99,173 | 1,244 | 18 | 1,262 | 821 | 6 | 827 |
| 2 | 97,911 | 1,626 | 12 | 1,638 | 2,066 | 24 | 2,089 |
| 3 | 96,273 | 1,582 | 49 | 1631 | 3692 | 36 | 3727 |
| 4 | 94,642 | 1472 | 76 | 1548 | 5273 | 85 | 5358 |
| 5 | 93,093 | 1264 | 65 | 1329 | 6745 | 161 | 6906 |
| 6 | 91,764 | 1316 | 89 | 1404 | 8009 | 227 | 8235 |
| 7 | 90,360 | 1237 | 85 | 1322 | 9325 | 315 | 9640 |
| 8 | 89,038 | 1092 | 141 | 1233 | 10,561 | 401 | 10,962 |
| 9 | 87,805 | 1098 | 139 | 1237 | 11,653 | 542 | 12,195 |
| 10 | 86,568 | 982 | 145 | 1126 | 12,751 | 681 | 13,432 |
| 11 | 85,441 | 806 | 168 | 974 | 13,733 | 826 | 14,558 |
| 12+ | 84,468 | 14,539 | 994 | 15,532 | |||
|
Example Remember that S(0) = 1 and therefore l0 = 100,000. In Table 7.2 the value of the survival function at duration one is 0.99173. Therefore lx = 100,000 x S(1) = 100000 x 0.99173 = 99173 The lx values for all durations are presented in column 2 of Table 7.3. We will use the lx column in Table 7.3 and the crude probability calculated in Table 7.2 to obtain the number of divorces and widowhoods at specified marital duration in the life table. For example, crude probability of divorce at duration zero is 0.008214 and the crude probability of widowhood at this duration is 0.0006. Therefore, number of divorces at duration zero in the life table population is:
Similarly the number of widowhoods at duration zero in this life table population is:
The number in still-intact marriages at duration one is l1 = 99173. The respective crude probabilities of divorce and widowhood at this duration are 0.01255 and 0.00018 Therefore, the number of divorces and widowhoods at duration 1 is obtained as follows:
Number of divorces and widowhoods at all durations are presented in Table 7.3. |
|||||||
Remark
The sum of the number of divorces and widowhoods at a specified marital duration gives the total number of marital disruptions at that duration. For example at duration zero there were 821 divorces and 6 widowhoods with a total of 827 marital disruptions. The total marital disruption at specified marital durations are shown in Column 5 of Table 7.3.
Step 6: Cumulative number of events of specified types
So far we have calculated the number of events of various types at specified times. Now we calculate the cumulative number of events of various types 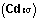 . By simply summing the number of events at each time point:
. By simply summing the number of events at each time point:
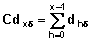

|
Example In Table 7.3 the number of divorces at duration zero is 821. The number of divorces at marital duration one is 1244. Therefore the cumulative number of divorces at the end of year one (beginning of year 2) is 821 + 1244 = 2065. Continuing the summation yields the cumulative number of divorces in this life table population at the beginning of each marital duration. Table 7.3 shows the cumulative number of divorces, widowhoods, and total marital disruptions at all marital durations. From the table one can see that, at the beginning of year 12, there were 14539 divorces, 894 widowhoods and 15532 marital disruptions in this life table population. |
Step 7: Cumulative probability of an event of specified type
In a life table with radix l0, the total number of events of a particular type occurring by time x is 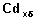
 . Therefore the probability that an individual will experience event
. Therefore the probability that an individual will experience event 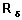 by duration x is
by duration x is 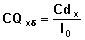
|
Example In Table 7.3, the cumulative number of divorces by marital duration 12 is 14539. Therefore the probability that a marriage will end due to divorce by year 12 is calculated as The cumulative probabilities for all durations are shown in Table 7.4. |
|
Table 7.4: Cumulative Probabilities of Divorce and Widowhood
|
||
| Duration of Marriage in Completed Years | CQxd | CQxw |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0.00821 | 0.00006 |
| 2 | 0.02066 | 0.00024 |
| 3 | 0.03692 | 0.00036 |
| 4 | 0.05273 | 0.00085 |
| 5 | 0.06745 | 0.00161 |
| 6 | 0.08009 | 0.00227 |
| 7 | 0.09325 | 0.00315 |
| 8 | 0.10561 | 0.00401 |
| 9 | 0.11653 | 0.00542 |
| 10 | 0.12751 | 0.00681 |
| 11 | 0.13733 | 0.00826 |
| 12+ | 0.14539 | 0.00994 |
Remark
So far we have learned to construct a multiple decrement life table with exact-time-to event data. The principal quantities we learned to compute and interpret are crude probabilities and the event type-specific cumulative probabilities.
The most often used data in the multiple decrement life tables are the cumulative probabilities. One may also want to look at the average time to an event of specific type. Median is the preferred measure. The median time for a specific event is defined as the duration at which the cumulative probability reaches one half (0.5). In the above example the cumulative probabilities of both divorce and widowhood are less than 0.5 at the maximum point of observation (12 years).
The next example extends the construction of multiple decrement life tables to grouped data.
Multiple Decrement Life Tables with Grouped Data
Following are some notations, computational formulas, and examples to illustrate the method. Most of the concepts have been introduced in the previous sections. Therefore a brief introduction is provided here.
Notations
n ~ the length of the class interval. The length need not be the same for each class interval.
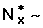 ~ Number of events of type
~ Number of events of type 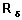 in the interval (x, x + n)
in the interval (x, x + n)
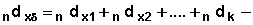 ~ Total number of events in the interval (x, x + n)
~ Total number of events in the interval (x, x + n)
(nCx) ~ Number censored in the interval (x, x + n)
Nx ~ Number in the risk set (exposed to the risk of an event) at the beginning of the interval (x, x + n)
By definition Nx + n = Nx — (nDx) — (nCx)
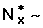 ~ Adjusted number in the risk set.
~ Adjusted number in the risk set.
We assume that censoring is uniform in the interval and calculate the adjusted risk set. The adjusted risk set at the beginning of each interval is computed by taking away half of the censored observations from the interval from the number who have not experienced any event at the beginning if each interval. Thus,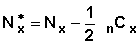
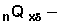 ~ Crude probability of an event of type
~ Crude probability of an event of type 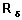 in the interval (x, x + n)
in the interval (x, x + n)
(nqx) ~ Probability of an event (regardless of type) in the interval (x, x+ n)
By definition:
(nqx) = (nQx1) + (nQx2) + ... + (nQxk)
Computational Formula
By definition:
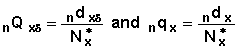
The survival function (the proportion of individuals experiencing no event until the beginning of the interval) is calculated by the Kaplan-Meier estimate as:

Recall that a quantity lx = 100,000 * S(x) and l0 = 100,000.
The number of events of a particular type 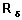 in the life table population is calculated as:
in the life table population is calculated as:
The cumulative number of events of type 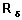 until the beginning of the interval (x, x + n) is equal to:
until the beginning of the interval (x, x + n) is equal to:
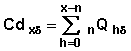
The cumulative probability of an event of particular type by the beginning of an interval is:
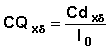
Example: Analysis of Oral Contraceptive Use Data
Earlier we constructed an ordinary life table to examine the duration of oral contraceptive use regardless of the reason for termination. In the multiple decrement life table we will differentiate the reasons for termination. Three reasons for discontinuation are identified in the data: Planning pregnancy, medical reasons, and others. The duration of use is tabulated in interval form. The data are reproduced in Table 7.5.
|
Table 7.5: Length of Use of Oral Contraceptives by Termination Reason
|
|||||||
Duration of Pill Use | Planning Pregnancy | Medical Reasons | Others | Terminations | Continuing Users | Nx | 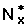 |
|---|---|---|---|---|---|---|---|
| 1-3 | 15 | 64 | 30 | 109 | 32 | 732 | 716.0 |
| 4-6 | 10 | 33 | 12 | 55 | 31 | 591 | 575.5 |
| 7-9 | 12 | 19 | 13 | 44 | 24 | 505 | 493.0 |
| 10-12 | 6 | 8 | 17 | 31 | 24 | 437 | 425.0 |
| 13-15 | 7 | 15 | 4 | 26 | 27 | 382 | 368.5 |
| 16-18 | 3 | 4 | 4 | 11 | 19 | 329 | 319.5 |
| 19-21 | 2 | 3 | 3 | 8 | 26 | 299 | 286.0 |
| 22-24 | 2 | 9 | 3 | 14 | 23 | 265 | 253.5 |
| 25-27 | 6 | 7 | 2 | 15 | 29 | 228 | 213.5 |
| 28-30 | 2 | 1 | 5 | 8 | 13 | 184 | 177.5 |
| 31-33 | 3 | 5 | 3 | 11 | 21 | 163 | 152.5 |
| 34-36 | 2 | 1 | 2 | 5 | 19 | 131 | 121.5 |
| 37-39 | 2 | 1 | 1 | 4 | 16 | 107 | 99.0 |
| 40-42 | 3 | 2 | 5 | 10 | 9 | 87 | 82.5 |
| 43-45 | 2 | 2 | 1 | 5 | 10 | 68 | 63.0 |
| 46-48 | 1 | 0 | 0 | 1 | 13 | 53 | 46.5 |
| 49+ | 2 | 1 | 0 | 3 | 36 | 39 | |
Step 1: Computation of Adjusted Risk Set
In Table 2.2 in the previous chapter we have already calculated the risk set and adjusted risk set for all the intervals considered. These numbers are reproduced in columns 7 and 8 of Table 7.5.
There were 732 women in the sample. Thirty two women were censored in the interval 1-3. Therefore the adjusted risk set is 732 - 0.5 * 32 = 716. One hundred nine women terminated the use of pill in the same interval. Therefore the number in the risk set at the beginning of the interval 4-6 is 732 - 109 - 32 = 591. There were 31 censored cases in the interval 4-6. Therefore the adjusted number in the risk set at the beginning of interval 4 is591 - 0.5 * 31 = 575.5. The risk set for other durations is shown in Table 7.5.
Step 2: Computation of Crude Probabilities
Recall that crude probabilities are calculated by dividing the number of events of a particular type by the adjusted number in the risk set. In the interval 1-3 there were 15 terminations due to planning pregnancy, 64 terminations due to medical reasons, and 109 terminations due to other reasons. The adjusted number in the risk set at the beginning of interval 1-3 is 716. Therefore the crude probabilities of terminations due to planning pregnancy, medical reasons, and other reasons are respectively
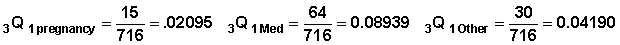
Table 7.6 shows the crude probabilities for all durations. The total probability of occurrence of an event in the interval (nqx) is the sum of all crude probabilities.
| Table 7.6: Crude Probabilities of Pill Discontinuation | |||||||
Duration of Pill Use | Qxpreg | QxMed | QxOther | qx | S(x) | ||
|---|---|---|---|---|---|---|---|
| 1-3 | 0.02095 | 0.08939 | 0.04190 | 0.152235 | 1.00000 | ||
| 4-6 | 0.01738 | 0.05734 | 0.02085 | 0.09557 | 0.84777 | ||
| 7-9 | 0.02434 | 0.03854 | 0.02637 | 0.08925 | 0.76675 | ||
| 10-12 | 0.01412 | 0.01882 | 0.04000 | 0.07294 | 0.69831 | ||
| 13-15 | 0.01900 | 0.04071 | 0.01085 | 0.07056 | 0.64738 | ||
| 16-18 | 0.00939 | 0.01252 | 0.01252 | 0.03443 | 0.60170 | ||
| 19-21 | 0.00699 | 0.01049 | 0.01049 | 0.02797 | 0.58099 | ||
| 22-24 | 0.00789 | 0.03550 | 0.01183 | 0.05523 | 0.56473 | ||
| 25-27 | 0.02810 | 0.03279 | 0.00937 | 0.07026 | 0.53355 | ||
| 28-30 | 0.01127 | 0.00563 | 0.02817 | 0.04507 | 0.49606 | ||
| 31-33 | 0.01967 | 0.03279 | 0.01967 | 0.07213 | 0.47370 | ||
| 34-36 | 0.01646 | 0.00823 | 0.01646 | 0.04115 | 0.43953 | ||
| 37-39 | 0.02020 | 0.01010 | 0.01010 | 0.04040 | 0.42145 | ||
| 40-42 | 0.03636 | 0.02424 | 0.06061 | 0.12121 | 0.40442 | ||
| 43-45 | 0.03175 | 0.03175 | 0.01587 | 0.07937 | 0.35540 | ||
| 46-48 | 0.02151 | 0.00000 | 0 | 0.02151 | 0.32719 | ||
| 49+ | 0.32015 | ||||||
Step 3: Calculation of the Survival Probabilities
Using the Kaplan-Meier formula yields the survival probabilities:
S(1) = 1 [Note that in the tabulated data the interval starts at one rather than zero.]
S(4) = 1 — (3q1) = 1 — 0.15223 = 0.84777
S(7) = S(4) * [1 — 3q 4] = 0.84777 * (1 — 0.09557) = 0.76675
The survival functions for all durations are shown in Table 7.6.
Step 4: Calculation of Life Table Survival Population
The radix of the life table l0 = 100,000
Then the lx column in the life table is calculated as lx = 100,000 * S(x)
In Table 7.6, S(4) = 0.76675. Therefore l4 = 100000 * 0.76675 = 76675
The lx values for all durations are shown in Table 7.7.
|
Table 7.7: Number of Pill Use Terminations by Cause
|
||||
Duration of Pill Use | lx | dxPregnancy | dxmed | dxother |
|---|---|---|---|---|
| 1-3 | 100,000 | 2095 | 8939 | 4190 |
| 4-6 | 84777 | 1473 | 4861 | 1768 |
| 7-9 | 76675 | 1866 | 2955 | 2022 |
| 10-12 | 69831 | 986 | 1314 | 2793 |
| 13-15 | 64738 | 1230 | 2635 | 703 |
| 16-18 | 60170 | 565 | 753 | 753 |
| 19-21 | 58099 | 406 | 609 | 609 |
| 22-24 | 56473 | 446 | 2005 | 668 |
| 25-27 | 53355 | 1499 | 1749 | 500 |
| 28-30 | 49606 | 559 | 279 | 1397 |
| 31-33 | 47370 | 932 | 1553 | 932 |
| 34-36 | 43953 | 724 | 362 | 724 |
| 37-39 | 42145 | 851 | 426 | 426 |
| 40-42 | 40442 | 1471 | 980 | 2451 |
| 43-45 | 35540 | 1128 | 1128 | 564 |
| 46-48 | 32719 | 704 | 0 | 0 |
| 49+ | 32015 | |||
Step 5: Cumulative Number of Events by Type
This step calculates the cumulative number of terminations of pill use by type at the end of the each interval (or to the beginning of the next interval). Forming simple sums with the number events of specific types 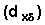 will complete this step.
will complete this step.
For example, in Table 7.7, the number of terminations due to pregnancy planning in the interval 1-3 is 2095 and the corresponding number for the interval 4-6 is 1473. The cumulative number of terminations for pregnancy planning at time 7 (which is the end of the interval) [Cd7 Pregnancy] is 2095 + 1473 = 3568. Cumulative numbers for all durations by types of termination are shown in Table 7.8.
|
Table 7.8: Cumulative Number of Events at the Beginning of the Interval
|
||||
Duration of Pill Use | Cdxpregnancy | CdxMedical | CdxOthers | Cdx |
|---|---|---|---|---|
| 1-3 | 0 | 0 | 0 | 0 |
| 4-6 | 2095 | 8939 | 4190 | 15223 |
| 7-9 | 3568 | 13800 | 5958 | 23325 |
| 10-12 | 5434 | 16755 | 7979 | 30169 |
| 13-15 | 6420 | 18069 | 10773 | 35262 |
| 16-18 | 7650 | 20704 | 11475 | 39830 |
| 19-21 | 8215 | 21458 | 12229 | 41901 |
| 22-24 | 8621 | 22067 | 12838 | 43527 |
| 25-27 | 9067 | 24072 | 13507 | 46645 |
| 28-30 | 10566 | 25821 | 14006 | 50394 |
| 31-33 | 11125 | 26101 | 15404 | 52630 |
| 34-36 | 12057 | 27654 | 16336 | 56047 |
| 37-39 | 12781 | 28016 | 17059 | 57855 |
| 40-42 | 13632 | 28442 | 17485 | 59558 |
| 43-45 | 15103 | 29422 | 19936 | 64460 |
| 46-48 | 16231 | 30550 | 20500 | 67281 |
| 49+ | 16934 | 30550 | 20500 | 67985 |
Step 6: Cumulative Probability of Pill Use Terminations by Cause
The cumulative probability of pill use terminations by cause is calculated by dividing the corresponding cumulative number of terminations by 100,000 (the radix of the life table).
Table 7.8 shows that the cumulative number of terminations at the beginning of month 49 is 16934, 30551, and 20500 respectively for pregnancy planning, medical reasons and other reasons. The corresponding cumulative probabilities are: 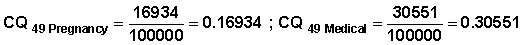
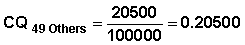
The cumulative probability of terminations of all types is the sum of all the type specific probabilities.
CQx = 0.16934 + 0.30551 + 0.20500 = 0.68285.
Remark
The above cumulative probabilities indicate that 68.3% of the women had stopped using the pill by month 49. Terminations by type show that 17.9% stopped because they are planning pregnancy, 30.5% terminated due to medical reasons, and 20.5% dropped due to other reasons. The cumulative probabilities for all durations are shown in Table 7.9.
|
Table 7.9: Cumulative Probability of Pill Use Terminations by Type
|
||||
| Duration of Pill Use | CQxpregnancy | CQxMedical | CQxOthers | CQx |
|---|---|---|---|---|
| 1-3 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| 4-6 | 0.02095 | 0.08939 | 0.04190 | 0.15223 |
| 7-9 | 0.03568 | 0.13800 | 0.05958 | 0.23325 |
| 10-12 | 0.05434 | 0.16755 | 0.07979 | 0.30169 |
| 13-15 | 0.06420 | 0.18069 | 0.10773 | 0.35262 |
| 16-18 | 0.07650 | 0.20704 | 0.11475 | 0.39830 |
| 19-21 | 0.08215 | 0.21458 | 0.12229 | 0.41901 |
| 22-24 | 0.08621 | 0.22067 | 0.12838 | 0.43527 |
| 25-27 | 0.09067 | 0.24072 | 0.13507 | 0.46645 |
| 28-30 | 0.10566 | 0.25821 | 0.14006 | 0.50394 |
| 31-33 | 0.11125 | 0.26101 | 0.15404 | 0.52630 |
| 34-36 | 0.12057 | 0.27654 | 0.16336 | 0.56047 |
| 37-39 | 0.12781 | 0.28016 | 0.17059 | 0.57855 |
| 40-42 | 0.13632 | 0.28442 | 0.17485 | 0.59558 |
| 43-45 | 0.15103 | 0.29422 | 0.19936 | 0.64460 |
| 46-48 | 0.16231 | 0.30550 | 0.20500 | 0.67281 |
| 49+ | 0.16934 | 0.30550 | 0.20500 | 0.67985 |
Summary
This example demonstrated how to construct a multiple decrement life table using event-time data in grouped form. The key parameters of interest are the cumulative probabilities of events by type for different durations. Intermediate steps in obtaining these parameters are calculation of adjusted risk set and crude probabilities of type-specific probabilities.
7.2 Assignment
The following information was collected in a demographic survey from ever-married women with no premarital birth. Women were asked about the date of birth of their first child or date of marital disruption whichever came first. Time from marriage to the event (either birth or marital disruption) was noted. For women who were in intact first marriage at the time of survey, time from marriage to the time of survey was noted. For these women the time to event is considered as censored at the duration of marriage at the time of survey. Data are tabulated in one-year intervals in Table 7.10.
| Table 7.10 | |||
| Time Since Marriage (Years) | Women with First Birth in the Year | Women Divorced Before First Birth | Childless Women in Intact Marriage at Survey |
|---|---|---|---|
| 0 | 3871 | 192 | 577 |
| 1 | 6263 | 190 | 466 |
| 2 | 2854 | 150 | 386 |
| 3 | 1560 | 86 | 261 |
| 4 | 981 | 85 | 185 |
| 5 | 602 | 61 | 141 |
| 6 | 325 | 45 | 110 |
| 7 | 238 | 34 | 64 |
| 8 | 161 | 26 | 55 |
| 9 | 102 | 22 | 58 |
| 10 | 89 | 28 | 34 |
| 11 | 65 | 18 | 37 |
| 12+ | 158 | 108 | 28 |
Assume that censoring is distributed uniformly within the one-year interval. For simplicity assume that all marital disruptions are due to divorce. With this assumption calculate:
- Number in the risk set at the beginning of each interval (Nx).
- Adjusted number in the risk set at the beginning of each interval
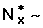 .
. - Crude probability of birth and divorce in each interval QxBirth, QxDivorce.
- Total probability of either birth or divorces in the interval (dxBirth, dxDivorce).
- Survival probability (probability neither birth or divorce occurring) (qx).
- Assume that l0 = 100,000 and complete lx column in the life table.
- Number of births and divorce in each interval in the life table population (dxBirth, QxDivorce).
- Cumulative number of births and divorces in each interval (CdxBirth, CdxDivorce).
- Cumulative probabilities of birth and divorce by the beginning of each interval (CQxBirth, CQxDivorce).
Interpret the results.
SEE ANSWERS IN TABLE 7.11 AND 7.12.
| Table 7.11 Crude Probabilities of Birth and Divorce | ||||||
| Time Since Marriage (Years) | Risk Set | Adjusted Risk Set | S(x) | qx | Qxdivorce | Qxbirth |
|---|---|---|---|---|---|---|
| 0 | 20716 | 20427.5 | 0.1895 | 0.02825 | 0.21775 | 1.00000 |
| 1 | 16076 | 15843 | 0.39532 | 0.02941 | 0.42473 | 0.78225 |
| 2 | 9157 | 8964 | 0.31838 | 0.04306 | 0.36145 | 0.45001 |
| 3 | 5767 | 5636.5 | 0.27677 | 0.04631 | 0.32307 | 0.28735 |
| 4 | 3860 | 3767.5 | 0.26038 | 0.0491 | 0.30949 | 0.19452 |
| 5 | 2609 | 2538.5 | 0.23715 | 0.05554 | 0.29269 | 0.13432 |
| 6 | 1805 | 1750 | 0.18571 | 0.06286 | 0.24857 | 0.095 |
| 7 | 1325 | 1293 | 0.18407 | 0.0495 | 0.23357 | 0.07139 |
| 8 | 989 | 961.5 | 0.16745 | 0.0572 | 0.22465 | 0.05471 |
| 9 | 747 | 718 | 0.14206 | 0.08078 | 0.22284 | 0.04242 |
| 10 | 565 | 548 | 0.16241 | 0.06204 | 0.22445 | 0.03297 |
| 11 | 414 | 395.5 | 0.16435 | 0.09355 | 0.2579 | 0.02557 |
| 12+ | 294 | 280 | 0.56429 | 0.10000 | 0.66429 | 0.01897 |
| Table 7.12 Cumulative Probabilities of Birth and Divorce | ||||||||||
| Time Since Marriage (Years) | lx | dxBirth | dxDivorce | dx | Cdxbirth | Cdx | CdxDivorce | CQxbirth | CQxDivorce | CQx |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 100000 | 18950 | 2825 | 21775 | 0 | 0 | 0 | |||
| 1 | 78225 | 30924 | 2301 | 33225 | 18950 | 2825 | 21775 | 0 | 0 | 0 |
| 2 | 45001 | 14328 | 1938 | 16266 | 49874 | 5126 | 55000 | 0.1895 | 0.02825 | 0.21775 |
| 3 | 28735 | 7953 | 1331 | 9284 | 64201 | 7064 | 71265 | 0.49874 | 0.05126 | 0.55 |
| 4 | 19452 | 5065 | 955 | 6020 | 72154 | 8394 | 80548 | 0.64201 | 0.07064 | 0.71265 |
| 5 | 13432 | 3185 | 746 | 3931 | 77219 | 9349 | 86568 | 0.72154 | 0.08394 | 0.80548 |
| 6 | 9500 | 1764 | 597 | 2362 | 80405 | 10095 | 90500 | 0.77219 | 0.09349 | 0.86568 |
| 7 | 7139 | 1314 | 353 | 1667 | 82169 | 10693 | 92862 | 0.80405 | 0.10095 | 0.905 |
| 8 | 5471 | 916 | 313 | 1229 | 83483 | 11046 | 94529 | 0.82169 | 0.10693 | 0.92862 |
| 9 | 4242 | 603 | 343 | 945 | 84399 | 11359 | 95758 | 0.83483 | 0.11046 | 0.94529 |
| 10 | 3297 | 535 | 205 | 740 | 85002 | 11702 | 96704 | 0.84399 | 0.11359 | 0.95758 |
| 11 | 2557 | 420 | 239 | 659 | 85537 | 11906 | 97443 | 0.85002 | 0.11702 | 0.96704 |
| 12+ | 1897 | 85958 | 12145 | 98103 | 0.85537 | 0.11906 | 0.97443 | |||
7.3 Calculation of Standard Errors
Because life tables are calculated with sample data it is desirable to know the variability in the estimated quantities in the life table. This section covers computation of the standard errors of various life table quantities. Some of the elements in the calculation of the standard errors are computationally involved.
1. Variance of 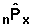 (Conditional probability of surviving the interval x, x+ n)
(Conditional probability of surviving the interval x, x+ n)
 , where
, where 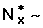 is the adjusted risk set at the beginning of the interval[x, x + n]. Standard error is the square root of the variance.
is the adjusted risk set at the beginning of the interval[x, x + n]. Standard error is the square root of the variance.
|
Example In Table 7.6, for the first interval: (3q1) = 0.15223; (3p1) = 1 — (3q1) = 1 — .15223; N1 = 716.0
Standard Error Similarly one can compute standard errors of all other conditional probabilities. The calculated standard errors are shown in Table 7.13.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2. Variance of Event-Specific Conditional Probabilities (equation )
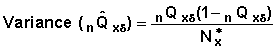
Standard error is the square root of the variance.
|
Example In Table 7.6: 3Q1Pregnancy = 0.02095 Therefore Standard Error Similarly one can calculate the standard error of pregnancy planning specific probabilities for other intervals. The calculated probabilities are shown in Table 7.13. |
For the computation of the variance of the cumulative probabilities it is necessary to calculate the covariance 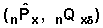 .
.
Covariance 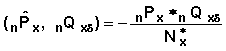 .
.
|
Example From Table 7.6: 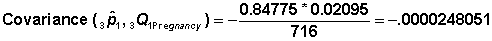 Table 7.13 shows covariance for all other intervals. |
4. Variance of Event-Specific Cumulative Probabilities 
Before presenting a general formula for event-specific Cumulative probabilities, we first look at some specific cases.
Case 1
The cumulative probability at the end of the first interval is simply the event specific probability in the first interval. So we can denote:
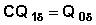
Therefore 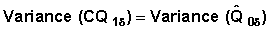
|
Example 1 From Table 7.6 CQ1Pregnancy = 0.02095. Variance |
Case 2
The event specific cumulative probability at the end of the second interval is:
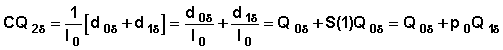
Therefore an approximate variance of the event-specific cumulative probability 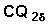 is obtained as:
is obtained as:
Variance of [SORRY, IMAGE 46-8.gif NOT AVAILABE]
Variance 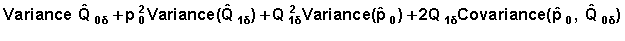
For simplicity we rewrite the above variance with some additional notations: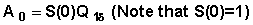 ; B0 = 1 and B1 = p0 (Note that S(1) = p0).
; B0 = 1 and B1 = p0 (Note that S(1) = p0).
Then the variance equation is expressed as:
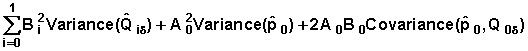
|
Example 2 From Table 7.6: From Table 7.13:
Taking square root yields:
|
Case 3
The event-specific cumulative probability to the end of the third interval is calculated as:
The variance of is approximated as: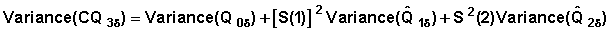
+ 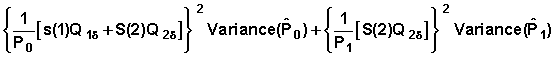
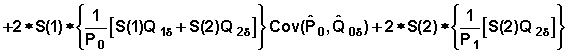
We rewrite this equation with symbols as before:
Denote: B0 = 1 B1 = S(1) B2 = S(2)
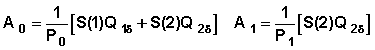
Then 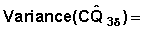
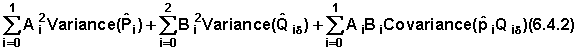
|
Example In Table 7.9: CQ3Pregnancy = 0.05434 Simple calculations gives: A0 = 0.039394 A1 = 0.02063449 B0 = 1 B1 = 0.84776 B2 = 0.76674
Substituting in the equation yields:
Taking square root we get
|
Case 4: A general formula for the event specific cumulative probabilities
A close look at equations 7.4.1 and 7.4.2 will reveal a pattern that will help in writing a general formula for the standard error of the cumulative probabilities. In general event-specific cumulative probability is denoted as 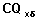 . Note that in this case x denotes the beginning of the interval (x, x+ n) or exact duration x. The computation is by the formula:
. Note that in this case x denotes the beginning of the interval (x, x+ n) or exact duration x. The computation is by the formula:
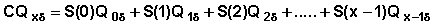
Then the variance of this computed quantity can be expressed as:

where
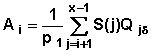 B1 = S(x) and B0 = 1
B1 = S(x) and B0 = 1
Calculations of the required quantities can be implemented through a spreadsheet.
We illustrate here the method for the steps for calculating the standard error of the cumulative probability of pill discontinuation in month 49 due to pregnancy planning.
In Table 7.9 we calculate this number as CQ16Pregnancy = 0.16934
[Note: Denoting interval 1-3 as zero and interval 4-6 as one and so on. the interval 49 or more will be 16.]
We will use equation 7.4.3 to obtain the variance of 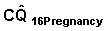 .
.
In the equation x = 16.
Therefore we need to calculate A0, A1, ....A14 and B0, B1, ....B15. The Bs are simply the survival function S(x)with S(0) = 1. Table 7.14 shows the calculation of the A values. Note that by definition
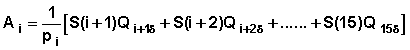
So simply cumulating the products 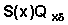 and dividing by the proper survival probability the quantities Ai can be calculated.
and dividing by the proper survival probability the quantities Ai can be calculated.
|
Table 7.14 Standard Error Calculation of
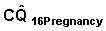 |
||||||
| i | Duration of Pill Use | Bi | S(x) QxPregnancy | 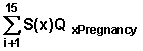 | Pi | Ai |
|---|---|---|---|---|---|---|
| 0 | 1-3 | 1.00000 | 0.0209497207 | 0.1483947937 | 0.84777 | 0.175042294 |
| 1 | 4-6 | 0.84777 | 0.0147309359 | 0.1336638578 | 0.90443 | 0.147787800 |
| 2 | 7-9 | 0.76675 | 0.0186631695 | 0.1150006882 | 0.91075 | 0.126270243 |
| 3 | 10-12 | 0.69831 | 0.0098585449 | 0.1051421434 | 0.92706 | 0.113414749 |
| 4 | 13-15 | 0.64738 | 0.0122975426 | 0.0928446008 | 0.92944 | 0.099892658 |
| 5 | 16-18 | 0.60170 | 0.0056497764 | 0.0871948243 | 0.96557 | 0.090303878 |
| 6 | 19-21 | 0.58099 | 0.0040628346 | 0.0831319897 | 0.97203 | 0.085524277 |
| 7 | 22-24 | 0.56473 | 0.0044554951 | 0.0786764946 | 0.94477 | 0.083275538 |
| 8 | 25-27 | 0.53355 | 0.0149942541 | 0.0636822406 | 0.92974 | 0.068494501 |
| 9 | 28-30 | 0.49606 | 0.0055894074 | 0.0580928332 | 0.95493 | 0.060834678 |
| 10 | 31-33 | 0.47370 | 0.0093187333 | 0.0487740999 | 0.92787 | 0.052565726 |
| 11 | 34-36 | 0.43953 | 0.0072351208 | 0.0415389791 | 0.95885 | 0.043321768 |
| 12 | 37-39 | 0.42145 | 0.0085140563 | 0.0330249228 | 0.95960 | 0.034415446 |
| 13 | 40-42 | 0.40442 | 0.0147060972 | 0.0183188256 | 0.87879 | 0.020845560 |
| 14 | 43-45 | 0.35540 | 0.0112824555 | 0.0070363701 | 0.92063 | 0.007642954 |
| 15 | 46-48 | 0.32719 | 0.0070363701 | |||
| 16 | 49+ | |||||
The required values of variances and covariances are given in Table 7.13.
Substituting the A and B values in Table 7.14 and the variances and covariances in Table 7.13 in the formula 7.4.3 we get the variance 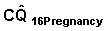 = 0.000406789. By taking the square root we get the standard error of
= 0.000406789. By taking the square root we get the standard error of  as 0.020169.
as 0.020169.
Use calculations similar to the one shown in Table 7.14 to get standard errors of the event specific cumulative probabilities for all durations. The final result is displayed in Table 7.15.
| Table 7.15: Standard Errors of Event-Specific (Pregnancy Planning) | |||
Interval Number | Duration of Pill Use |  | Standard Error  |
|---|---|---|---|
| 0 | 1-3 | 0.0000000 | |
| 1 | 4-6 | 0.000028646 | 0.0053522 |
| 2 | 7-9 | 0.000051150 | 0.0071519 |
| 3 | 10-12 | 0.000079329 | 0.0089067 |
| 4 | 13-15 | 0.000093574 | 0.0096734 |
| 5 | 16-18 | 0.000114376 | 0.0106947 |
| 6 | 19-21 | 0.000123593 | 0.0111172 |
| 7 | 22-24 | 0.000131095 | 0.0114497 |
| 8 | 25-27 | 0.000140457 | 0.0118515 |
| 9 | 28-30 | 0.000176920 | 0.0133011 |
| 10 | 31-33 | 0.000189327 | 0.0137596 |
| 11 | 34-36 | 0.000216772 | 0.0147232 |
| 12 | 37-39 | 0.000240747 | 0.0155160 |
| 13 | 40-42 | 0.000274396 | 0.0165649 |
| 14 | 43-45 | 0.000341488 | 0.0184794 |
| 15 | 46-48 | 0.000400410 | 0.0200102 |
| 16 | 49+ | 0.000447663 | 0.0211580 |
Exercise
Calculate the standard errors of the cumulative probabilities of pill termination due to medical reasons(CQxMedical) and other reasons (CQxOther) in Table 7.9.

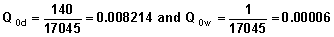
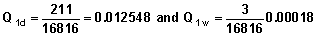
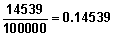 . The probability that a marriage will end due to widowhood by year
. The probability that a marriage will end due to widowhood by year 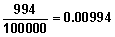
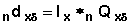
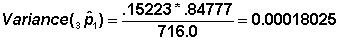
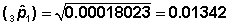
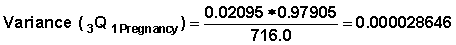
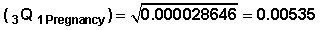 .
.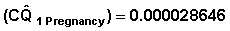
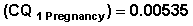
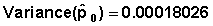


 )
)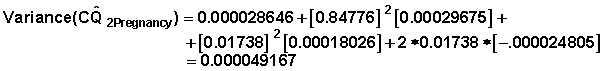
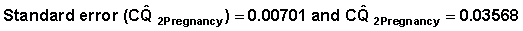 = 0.00701 and = 0.03568
= 0.00701 and = 0.03568