Lesson 5: Expectation of Life at Birth
5.0 Overview
Often expectation of life (ex0), and in particular expectation of life at birth e00, is considered to be a summary measure of mortality. Hence, differences in expectation of life (either between gender or other subgroups of population or between two time points) are considered to be indicators of changes in mortality. However, a change in life expectancy does not mean that the age-specific mortality rates change in the same magnitude and direction. Also, the contributions of various causes of death in the changes in expectations of life will not be of the same magnitude and direction. Some age-cause-specific death rates will increase in the two groups compared, thus contributing to a decrease in expectation of life, while others may decrease in some age intervals, thus increasing expectation of life.
Several authors have attempted to disentangle the contributions by age-specific and age-cause-specific death rates to the difference between two expectations of life. Applying these methods we learn to interpret the dynamics of changes in the mortality.
This lesson presents two methods to decompose changes in expectation of life at birth. The method developed by Arriaga (Arriaga, E. 1984. "Measuring and Explaining the Change in Life Expectancies," Demography 21: 83-96) is described first (Section 5.1). The second method was developed by Pollard (Section 5.2) (Pollard, J. H. 1988. "On the Decomposition of Changes in Expectation of Life and Differentials in Life Expectancy," Demography25(2): 265-276). Pollard's method is an exact decomposition developed using a continuous modeling approach of the life table, whereas Arriaga's method is based on the discrete analysis approach. As such, Arriaga's method is an approximate method and is easier to compute. (Refer to the papers for details.)
The final section of this lesson (5.4) explains cause elimination life tables, which yield answers to the hypothetical questions about a cohort's mortality experience if a particular cause (or causes) were eliminated.
Download a zip file containing data for Lesson 5 in Excel and CSV formats.
5.1 Arriaga Method
Assume that we would like to compare the life expectancy of two groups (males and females, for example). Designate the two groups as Group 1 and Group 2. The goal is to decompose the difference in the expectation of life at birth to reveal the differences in age-specific death rates (and age-cause-specific death rates). We approach this problem in two steps: In Step 1, we will examine the contributions of the differences in age-specific death rates toward the changes in expectation of life at birth. In Step 2, we will extend this to include age-cause-specific death rates.
| e001 | ~ expectation of life at birth for group 1 |
| e002 | ~ expectation of life at birth for group 2 |
| ex0i | ~ expectation of life at age x in group i ( i = 1, 2) |
| lxi |
~ number of survivors to age x in group i ( i = 1, 2) |
| nLxi | ~ person years of life contributed in the age group ( x, x + n) in group i ( i = 1, 2) Note: See note above. This term is also expressed as a proportion in the table and calculations below. |
| Notation | Definition |
|---|
Arriaga's Formula
Step 1: Age-Specific Decomposition
Arriaga formulates the differences in the expectation of life at birth ( e002- e001) due to differences in age-specific death rates as:
|
|
|
||
|
Total effect
of age x = |
direct effect of age x + indirect effect of age x (summed over all age intervals) | |||
where
| direct effect of age (x , x + n) | ||||||
|
(DEx) =
|
|
|||||
and
| indirect effect of age (x , x + n) | ||||
|
(IEx) =
|
|
|||
The direct effect on life expectancy is due to the changes in life years within a particular age interval as a consequence of the mortality change in that age interval.
The indirect effect consists of the number of life years added to a life expectancy because of the changes in the number of survivors at the end of the age interval caused by the change in mortality within the age interval.
For an open-ended interval (x+), the contribution of the indirect effect is considered to be 0. Therefore, the total effect of this age interval is calculated as:
| DEx+ = lx1 [ex+ 02 - ex+ 0 1 ] |
|
Example The data necessary for decomposing the difference in expectations of life at birth of males and females in Costa Rica in 1960 are given in Table 5.1.1 below. From that table: Expectation of life at birth for males (call it e001) = 62.97 Difference (e002 - e001) = 65.44 - 62.97 = 2.47 The first goal is to calculate the contribution of the male-female differences in each age interval to a total difference of 3.04 years in expectation of life at birth. For this purpose, we calculate the direct effect and indirect effect of each age interval using the formulas above. First, let's look at a specific age interval, 20-24. From the table:
Direct effect of age group 20-24:
Indirect effect of age group 20-24:
Total effect = direct effect + indirect effect = 0.00589 + 0.11330 = 0.11961 (using rounded values, 0.11920 actual) Calculations show that the mortality rates in the age interval 20-24 contribute 0.1222 to a total change in expectation of life at birth of 3.04 years. The lower mortality rate for females in this age group is responsible for this positive contribution. The majority of this contribution of 0.11920 comes from the indirect effect: more females surviving to the next age interval. The contributions of mortality rates in all age intervals are in shown Table 5.1.1. Note that in age intervals 1-4, 25-29, and 30-34 the contributions are negative because of higher death rates for females in those age intervals. The biggest contribution is in the youngest age interval, <1. The gap between male-female mortality widens after age 40.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Step 2: Age-Cause-Specific Decomposition
In this section we will extend the decomposition of the difference in expectation of life at birth by further decomposing the change by age and causes of death. This decomposition is accomplished as follows:
- Calculate the proportion of change in the cause-specific mortality rates as a share of the total mortality change in the specific age interval.
- Distribute the calculated total effect into specific cause contributions according to the proportions calculated in Step a.
5.2 Pollard Method
Pollard (1988) proposed a method to decompose the difference in expectation of life at birth to determine the contribution of the difference in age and cause-specific mortality rates.
Unlike the Arriaga method, the Pollard method is based on the exact relationship between expectation of life at birth and age-specific mortality rates (some details are not shown here).
In this section we learn to apply Pollard's method of calculations.
Pollard's Formula
Pollard showed the following relationship between the difference in expectation of life at birth and the difference in age-specific death rates:
| e002 - e001 = | ¥ ó õ 0 |
[m(t,1) - m(t,2)]w(t)dt |
where m(t, 1) and m(t, 2) are the age-specific death rates and
|
For a specific age interval (x, x+n) the contribution is calculated as:
|
|
where nmx1 and nmx2 are age specific death rates in the age interval (x, x+n) and
|
To implement the calculations for each age interval (except for the open-ended interval), one will calculate an average weight as
| Average weight for age interval (x, x+ n) = | n 2 |
[w(x) + w(x + n)]
|
For an open-ended interval (x+) the average weight is calculated as:
|
where mx+1 and mx+2 denote the age-specific death rates of the open-ended age interval x+ |
The calculations of the average weight for different age intervals are illustrated in Table 5.2.1.
|
Table 5.2.1: Average Weight Calculations for 1960 Costa Rican Males and Females, Pollard Method
|
||||||||
| Age | lx1 | e01 | nmx2 | e02 | w(x) | w(x+n) | Avg. Weight | |
|---|---|---|---|---|---|---|---|---|
| 0 | 1.00000 | 62.97 | 0.0640 | 65.44 | 64.20488 | 63.22912 | 63.71700 | |
| 1 | 0.92770 | 66.84 | 0.0077 | 68.73 | 63.22912 | 59.55371 | 245.56565 | |
| 5 | 0.90204 | 64.69 | 0.0017 | 66.81 | 59.55371 | 55.04361 | 286.49330 | |
| 10 | 0.89436 | 60.22 | 0.0010 | 62.35 | 55.04361 | 50.56409 | 264.01925 | |
| 15 | 0.88867 | 55.59 | 0.0008 | 57.64 | 50.56409 | 46.10860 | 241.68171 | |
| 20 | 0.88298 | 50.93 | 0.0013 | 52.87 | 46.10860 | 41.68188 | 219.47619 | |
| 25 | 0.87504 | 46.37 | 0.0018 | 48.19 | 41.68188 | 37.29248 | 197.43591 | |
| 30 | 0.86792 | 41.73 | 0.0023 | 43.60 | 37.29248 | 32.94533 | 175.59453 | |
| 35 | 0.85938 | 37.12 | 0.0028 | 39.06 | 32.94533 | 28.65060 | 153.98982 | |
| 40 | 0.84651 | 32.65 | 0.0029 | 34.57 | 28.65060 | 24.42252 | 132.68280 | |
| 45 | 0.82802 | 28.32 | 0.0046 | 30.05 | 24.42252 | 20.29097 | 111.78374 | |
| 50 | 0.80173 | 24.17 | 0.0070 | 25.69 | 20.29097 | 16.29820 | 91.47294 | |
| 55 | 0.76558 | 20.19 | 0.0105 | 21.52 | 16.29820 | 12.50084 | 71.99761 | |
| 60 | 0.71583 | 16.43 | 0.0188 | 17.54 | 12.50084 | 9.00558 | 53.76604 | |
| 65 | 0.63605 | 13.18 | 0.0288 | 14.03 | 9.00558 | 5.95147 | 37.39261 | |
| 70 | 0.53040 | 10.32 | 0.0462 | 10.82 | 5.95147 | 3.45550 | 23.51743 | |
| 75 | 0.40933 | 7.67 | 0.0678 | 8.00 | 3.45550 | 1.60647 | 12.65494 | |
| 80 | 0.27931 | 5.14 | 0.1329 | 5.28 | 1.60647 | 0.48258 | 5.22263 | |
| 85+ | 0.14207 | 2.97 | 0.3164 | 3.16 | 0.48258 | 0.00000 | 1.48193 | |
Example
For age group 20-24:
where
and
Thus, average weight for the age interval 20 -24:
And average weight for open-ended interval 85+:
Contribution of difference in age-specific mortality rates of a specific age interval (x, x + n) to the difference in expectation of life at birth: [ nmx1 - nmx2 ] * average weight For age interval 20-24: [0.00181-0.0013] * 219.47619 = 0.11778 The age interval 20-24 contributes 0.11778 years to the total difference of 3.04 years in expectation of life at birth between males and females. Similarly, the contributions for all age intervals are computed and presented in Table 5.2.2. The youngest and the oldest age intervals are the highest contributors to the male-female differences in expectation of life at birth.
Contributions by Causes of DeathThe contributions by "all causes" of mortality can be decomposed into cause-specific contributions very easily using the Pollard method. Remember that age-specific mortality rate is equal to the sum of age-cause-specific mortality rates over all causes. Therefore, the difference in age-specific mortality also sums to the difference in age-cause-specific mortality rates. Using the symbols above:
where mxd denotes the age-specific death rates by cause Rd. Thus, the contribution of a specific cause Rd can now be expressed as:
5.3 Comparison of Arriaga and Pollard MethodsThe Pollard Method is analytically more exact. However, the Arriaga Method is conceptually simple, its components such as direct and indirect effects are easy to interpret, and it is easy to compute. Table 5.3.1 below gives the contribution from "all causes" to the difference in expectation of life at birth as calculated by both Pollard and Arriaga methods. In this example, the two methods achieve similar results; discrepancies occur from the approximations used in the computations. Also, Table 5.3.2 shows that the two methods achieve similar results in determining the total contributions for each of the four causes. However, discrepencies can occur when broader age intervals are used because of the discrete approximations used in the computations.
Exercise 14For this exercise, download the zip file and use the data file with the age-specific and age-cause-specific death rates and life tables for Taiwanese males in 1960 and 1964 (presented in tables below). Let the 1960 data be "Group 1" in your calculations and the 1964 data be "Group 2." Use your spreadsheet software to complete this exercise. Use these data tables to compute the contributions of each cause of mortality in determining the changes in expectation of life at birth between these periods. Use both the Arriaga Method and the Pollard Method and compare these methods.
After you finish the exercise, check your work with the answer key below. 5.4 Cause Elimination Life Tables and Gains in Expectation of LifeCause elimination life tables answer the hypothetical questions about a cohort's mortality experience if a particular cause (or causes) were eliminated. The gain in expectation of life after a particular cause of death is eliminated gives a summary measure of the impact of a particular cause of death in the population. When all the causes except a particular cause are eliminated (i.e. all competing causes are eliminated) the resulting cause-eliminated life table gives a life table that can be used to compare the mortality with respect to the selected cause across populations and across time. This comparison is possible because the resulting life table in this situation adjusts for the differences in the intensity of all other competing causes of death among the different populations. There are a number of methods available to construct life tables eliminating certain causes of death. A number of methods are described in Namboodiri and Suchindran (1987). This session briefly describe one simple method. This method is consistent with the method attributed to Fergany and used in the construction of the life table in Section 3.2. Life Table Construction Eliminating a Specified CauseRecall that in Section 3.2 under the assumption of constant mortality the relationship between proportion dying in an age interval (nqx) and the age-specific death rate (nmx) is expressed as: Also recall that the age-specific death rate is related to age-cause-specific death rates ( nmxd ) as:
In the hypothetical situation when one particular cause Rdis eliminated from the population, the age-specific death rate in the population will change to
The life table eliminating the cause Rdis calculated using the method in Lesson 3.2 with the assumption that the prevailing age-specific mortality in the population is nmx* . Specifically:
Exercise 151. For the 1960 Costa Rican males, construct a life table eliminating CVD as a cause of death and add a final column showing the gain in expectation of life for each age after eliminating CVD as a risk. Practical Suggestions:
2. Using your spreadsheet, show that the gain in expectation of life at birth when cancer is eliminated as a cause of death is 2.37 years. When you have finished the exercise, compare your calculations, graphs, and descriptions to the answer key below. Answers to ExercisesExercise 14Use these data tables to compute the contributions of each cause of mortality in determining the changes in expectation of life at birth between these periods. Use both the Arriaga Method and the Pollard Method and compare these methods. Note: Our starting point is the Expectation of Life Improvement for Newborns in Taiwan from 1960 (62.28) to 1964 (64.53) = 2.25
As you can see, the two methods produced very similar results over all causes. Now we look at this issue on a cause-by-cause basis:
The two methods produce very similar results. This table shows that "other causes" contributed the most to the improvement in expected life for the Taiwanese from 1960 to 1964. Reductions in CVD and tuberculosis mortality rates also contributed to the improvement. Cancer risks actually increased and had a negative effect on the mortality improvement. Exercise 151. For the 1960 Costa Rican males, construct a life table eliminating CVD as a cause of death and add a final column showing the gain in expectation of life for each age after eliminating CVD as a risk.
As you can see from the table, the gain in expectation of life after eliminating CVD as a risk factor ranges from 3.26 extra years at birth to 1.65 extra years in the 85+ age group. 2. Using your spreadsheet, show that the gain in expectation of life at birth when cancer is eliminated as a cause of death is 2.21 years. The table below is identical to the table above except cancer has been eliminated instead of CVD. At the top of the far right column, you can see the foreshadowed gain of 2.37 extra years at birth from eliminating cancer as a risk for 1960 Costa Rican Males.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
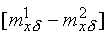* Average weight
